Resuelve los siguientes problemas:
1Indica el área de un círculo de 10 cm de diámetro, redondeando a dos cifras decimales.
cm2
¿Cuál sería la longitud de la circunferencia correspondiente? Redondea también a dos cifras decimales.
cm
Como el diámetro es 10 cm el radio es igual a 5 cm


El área del círculo es 78.54 cm2 y la longitud de la circunferencia es 31.42 cm
2En una imprenta hacen pegatinas para discos de música de forma que se cubra la parte superior del CD. Sabiendo que el radio mayor mide 5.8 cm y el menor 0.7 cm aproximadamante, ¿qué área de papel utilizan para cada CD?
cm2

El área de cada pegatina es 104.14 cm2.
3Calcula el área de un sector circular de angulo 45º sabiendo que la longitud de la circunferencia a la que pertenece mide 6Π.
cm2

4Para una fiesta de cumpleaños un grupo de 12 amigos compran una tarta de 28 cm de diámetro. Si dividimos el pastel en 12 porciones iguales, ¿qué área de tarta se come cada uno?
cm2
Como el diámetro mide 28 cm el radio mide 14 cm.
Dividimos la tarta en 12 porciones iguales, por tanto:

Cada trozo tiene como área 102.62 cm2.
5Sobre un círculo de 25Π cm2 de área trazamos un ángulo central de 90º. Calcula el área del segmento circular comprendido entre la cuerda que une los extremos de los dos radios y su arco correspondiente
cm2

Calculamos el área del segmento circular:

6Calcular el área de la zona coloreada de las siguientes figuras siendo la altura del rectángulo la mitad que la base.Redondea a dos cifras decimales.

cm2

cm2
 La primera figura es un hexágono con una circunferencia circunscrita, por tanto el área pedida será el área del hexágono menos el área de la circunferencia.
La primera figura es un hexágono con una circunferencia circunscrita, por tanto el área pedida será el área del hexágono menos el área de la circunferencia.
Calculamos la apotema que es el radio de la circunferencia y además la necesitamos para el área del hexágono.

 La segunda figura es un rectángulo con dos circunferencias inscritas, por tanto el área pedida será el área del rectángulo menos el área de las circunferencias.
La segunda figura es un rectángulo con dos circunferencias inscritas, por tanto el área pedida será el área del rectángulo menos el área de las circunferencias.
La altura del rectángulo es el diámetro de la circunferencia, su valor es 9 cm, por tanto el radio mide 3 cm

7El radio mayor de un roscón de reyes es de 20 cm mientras que el radio menor mide 7 cm. Si cortamos un trozo con un ángulo de 25º, ¿qué área del roscón hemos cortado?.
cm2

El área cortada es de 61.26 cm2.
8Calcular el área de la zona coloreada redondeando a dos cifras decimales
cm2
El área de la zona coloreada es el área del cuadrado menos el área del sector circular, cuyo ángulo es de 90º.

Si tienes dudas puedes consultar la teoría
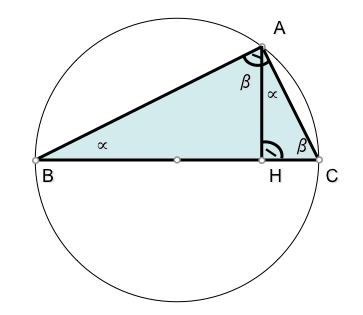









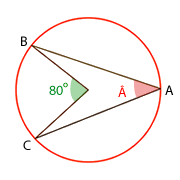
 es el suplementario de
es el suplementario de  , por tanto mide 150º.
, por tanto mide 150º.

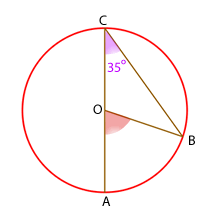
 mide 35º, como el triángulo ACO es isósceles, ya que dos de sus lados son los radios (por tanto iguales). Como los lados de un triángulo deben sumar 180º los ángulos del triángulo miden 35º, 35º y 110º
mide 35º, como el triángulo ACO es isósceles, ya que dos de sus lados son los radios (por tanto iguales). Como los lados de un triángulo deben sumar 180º los ángulos del triángulo miden 35º, 35º y 110º
 es inscrito medirá:
es inscrito medirá: º
º  º
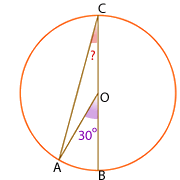
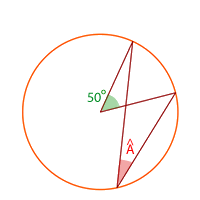
º  = 30º ya que es un ángulo inscrito y su arco es una división
= 30º ya que es un ángulo inscrito y su arco es una división = 60º ya que es un ángulo inscrito y su arco son dos divisiones
= 60º ya que es un ángulo inscrito y su arco son dos divisiones = 180º − (30º + 60º) = 90º
= 180º − (30º + 60º) = 90º
