Junto con
los conceptos de protencia , la geometría del triángulo rectángulo permite resolver la
obtención de medias proporcionales
Media
proporcional
Dada la
relación matemática x/a=b/x llamamos media proporcional al valor de x,
es decir
x= raíz
cuadrada de a*b
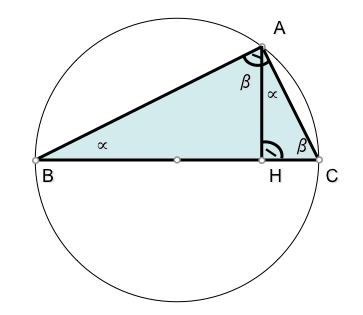
Podemos
obtener un triángulo rectángulo utilizando como hipotenusa un diámetro
de una circunferencia, y como vértice opuesto un punto de la misma, ya que
determina un arco capaz de 90 ° sobre dicho diámetro.
Si obtenemos
la altura h del triángulo desde el ángulo recto (vértice A) y
determinamos su intersección H con la hipotenusa (pie de la altura)
podemos determinar tres triángulos rectángulo semejantes:
- ABC
- HAC
- HBA
Teoremas de
la altura y del cateto
Aplicando
Thales a estos tres triángulos podemos obtener las siguientes relaciones:
Teorema
del cateto
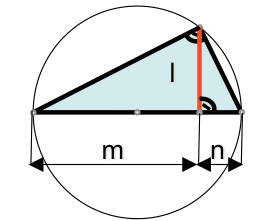
El cateto de
un triángulo rectángulo es media proporcional entre la hipotenusa y la
proyección de dicho cateto sobre la hipotenusa.
l*l=m*n
Teorema
de la altura
La altura de
un triángulo rectángulo medida sobre su hipotenusa es media proporcional entre
los dos segmentos en que la divide.
l*l=m*n

No hay comentarios:
Publicar un comentario